Il sistema altazimutale

Il sistema altazimutale (o orizzontale) si basa sull’orizzonte visivo dell’osservatore, considerato come un piano passante per il centro della Terra. Al piano sono associati due poli: lo zenit, situato sopra la verticale dell’osservatore, e il nadir, posto in direzione opposta.

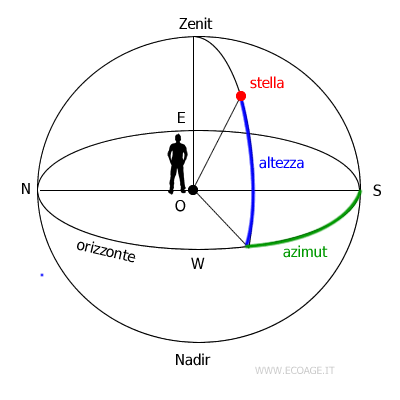
Per determinare la posizione di un astro nel cielo il sistema utilizza due coordinate angolari:

• L’altezza
  L’altezza è l’arco compreso tra l’astro e la linea dell’orizzonte. Si misura in gradi, primi e secondi e varia da 0° a 90°. È pari a 0° quando l’astro si trova sull’orizzonte ed è pari a 90° quando si trova allo zenit.
• L’azimut
  L’azimut è l’arco dell’orizzonte compreso tra il punto cardinale Sud e il circolo verticale passante per l’astro. Si misura in gradi, primi e secondi da 0° a 360°, procedendo in senso orario, cioè dal Sud verso Ovest (W).

Il sistema altazimutale presenta alcune limitazioni. Le coordinate di uno stesso astro cambiano infatti con la posizione geografica dell’osservatore e, anche rimanendo nel medesimo luogo, variano con l’ora di osservazione a causa della rotazione terrestre.

Nonostante ciò, il sistema altazimutale è molto utile perché descrive le posizioni degli astri così come appaiono nel cielo a un osservatore reale. Quindi, è molto intuitivo e immediato nell’osservazione pratica.

Esempio pratico

Alle 22:15 a Roma, un osservatore punta il cielo verso una stella situata a circa metà strada tra l’orizzonte e lo zenit. Misura l’angolo verticale e ottiene un’altezza di 45°.

Traccia il suo circolo verticale e misura l’arco sull’orizzonte a partire dal Sud in senso orario, fino a trovare l'intersezione di quel circolo con l'orizzonte, ottenendo un azimut di 220°.

In questo caso, si può affermare che alle 22:15 a Roma, la posizione della stella si trova a h = 45° (altezza) e A = 220° (azimut) nel sistema altazimutale.

In altre parole, questo significa che la stella si trova a 45° sopra l’orizzonte verso Nord-Est.

E così via.